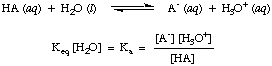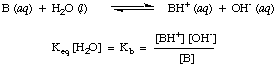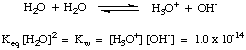Redox Reactions / Oxidation and reduction reactions
These are reactions where electrons are transferred from one species (atom, molecule or ion) to another. We can write 'half' equations to show only what happens to the species losing electrons or a different 'half' equation to show the species gaining electrons.
The whole equation is put together by making sure that the numbers of electrons are balanced in each half equation and adding them together (when the electrons will cancel out)
Oxidation
This is the name given to removal of electrons from a species - the reagent causing the loss of electrons is called the oxidising agent
| Example:
Mg(s)
In this (half) equation the magnesium atom loses
electrons and becomes an ion.
|
This is the gain of electrons - the species donating the electrons is called the reducing agent
| Example
Fe3+ + 3e
In this (half) equation the iron(III) ion gains
three electrons to become an atom.
|
Obviously the electrons leave one species and go to another. Consequently reduction has to be accompanied by oxidation and vice versa. For this reason reactions involving transfer of electrons are called reduction and oxidation or redox for short
| Example
3Mg(s) + 2Fe3+
The electrons from the magnesium are transferred
to the iron(III) ions
|
Loss of electrons = Oxidation
Gain of electrons = Reduction |
Mnemonic (memory aid)
OIL-RIG |
 |
|
Oxidation Is Loss
Reduction Is Gain |
10.1.2: Calculate the oxidation number of an element
in a compound. Oxidation numbers should be shown by a sign (+ or -) and
a number, eg +7 for Mn in KMnO4.
Oxidation number
This is the apparent valency of an atom within a compound. It is usually considered as if the element were bonded ionically to allow the apparent number of electrons gained or lost to be assessed.
The sum of all the oxidation numbers in a compound must add up to 0. By convention, the oxidation number is written as a Roman numeral in the name, eg. iron II sulphate, sulphur VI oxide.
The oxidation number of an uncombined element is always zero (0)
Calculating the oxidation number
There are some elements that virtually always have the same oxidation number and these can be used to calculate the oxidation numbers of the atoms in question.
Hydrogen, for example always has an oxidation number of -1 when bonded to a metal (more electropositive element) and +1 when bonded to a more electronegative element (non-metal). Oxygen is always -2 (except when in the form of the peroxide ion when it has an O-O bond giving it an oxidation number of -1). Group 1 and 2 metals usually have an oxidation number of 1+ and 2+ respectively.
| Example - Calculate the oxidation number of sulphur
in sulphuric acid H2SO4 Hydrogen = +1 oxidation number Oxygen = -2 oxidation number Therefore:
(2 x H) + S + (4 x O) = 0
2 + S -8 = 0
S = 6
|
| Example - Calculate the oxidation number of nitrogen
in calcium nitrate Ca(NO3)2 Calcium is in group 2 = +2 oxidation number Oxygen = -2 oxidation number Therefore:
(+2) + [(2 x N) + (6 x -2)] = 0
+2 + 2N -12 = 0
2N = 10
N = +5
|
10.1.3: State and explain the relationship between
oxidation numbers and the names of compounds. Oxidation numbers in names
of compounds are represented by Roman numerals, eg iron(II) oxide, iron(III) oxide.
Names of compounds
Where there is any doubt about the oxidation state of an element within a compound it is stated using Roman numerals immediately after the ambiguous element. For example Iron compounds may be iron in the oxidation state +2 or +3 - it must therefore be stated as iron II or iron III in the compound name.
In the examples above the full systematic name for sulphuric acid is sulphuric(VI) acid and calcium nitrate is calcium nitrate(V)
| Example - Name the following compound - FeSO4 Oxidation state of the oxygen = -2 Oxidation state of the sulphur = +6 Therefore oxidation state of the iron = - (+6 - 8) = +2 The name of the compound FeSO4 is iron(II) sulphate |
| Example - Name the following compound - TiCl4 Oxidation state of the chloride = -1 Therefore oxidation state of the titanium = - (- 4) = +4 The name of the compound TiCl4 is titanium(IV) chloride |
10.1.4: Identify whether an element is oxidised or
reduced in simple redox reactions, using oxidation numbers. Appropriate
reactions to illustrate this can be found in topics 3 and 11. Possible
examples include: iron(II) and (III), manganese(II) and (VII), chromium(III)
and (VI), copper(I) and (II), oxides of sulphur and oxyacids, halogens
and halide ions.
Oxidation and reduction
As stated above, for the purposes of oxidation and reduction the oxidation number can be thought of as the apparent ionic charge of an atom within a compound. For example, in sulphuric acid the sulphur is in the VI (6+) oxidation state. For the purposes of redox we can consider that it has an ionic charge of +6 (even though it is clearly covalently bonded). This makes it easier to follow any transfer of electrons.
If the sulphur changes to an oxidation state of IV during a chemical reaction then it has gone from an apparent ionic charge of +6 to a charge of +4, i.e. it has gained two electrons (negative charges). It has therefore been reduced (gain of electrons) in the process.
Examples
|
10.1.5: Define the terms oxidising agent and reducing
agent.
Oxidising agents
These are the chemicals that cause the oxidation in a redox reaction. We call the reacting compounds in a reaction the reagents (short form of the words reacting agents).
We consider that the removal of electrons from a species is oxidation and these electrons have to be taken away by another compound or species. This species that attracts the electrons is said to be the oxidising agent i.e. the reagent that causes the oxidation.
Reducing agents
Similarly the reagent that causes reduction in a redox reaction is said to be the reducing agent.
The oxidising agent takes the electron and is itself reduced, the reducing agent loses the electrons and is itself oxidised.
2KI
|
+ Br2
|
2KBr
|
+ I2
|
|
Iodide ions get oxidised
|
Bromine gets reduced
|
|||
Iodide - reducing agent
|
Bromine - oxidising agent
|
|||
Cr2O72-
|
+ 3SO2 +
2H+
|
2Cr3+
|
+ 3SO42-
+ H2O
|
|
| Chromium VI gets reduced | Sulphur IV gets oxidised | |||
| Chromium VI oxidising agent | Sulphur IV reducing agent | |||