Fundamentals of Acid-Base Chemistry
Definitions of Acidity and Basicity
For more than two-hundred years, chemists have struggled to come up with a
way to describe acid-base reactions that is at the same
time physically relevant, specific enough to be accurate, and general
enough to include everything that
should be considered an acid-base relationship.
Svante Arrhenius first defined acids to be proton (H
+) donors and
bases to be hydroxide ion (OH
-) donors in aqueous solution. The
Arrhenius model of
acids and bases is summarized by the following two reactions:
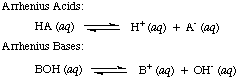
Figure %: The Arrhenius model of acids and bases, where A = acid and B = base
At the time that Arrhenius proposed these definitions, water was virtually the
only solvent
used in chemistry, and nearly
all known acids and bases contained protons (H
+) and hydroxyl groups
(OH), respectively. His definition was sufficient for the chemistry that was
understood then. But progress in chemistry necessitated new definitions: it was
discovered that ammonia behaves like a base, and HCl donates protons in
non-aqueous solvents. The Bronsted-Lowry model of acids
and bases serves that
need by describing acids as proton donors and bases as proton
acceptors. These definitions
remove the role of solvent and allow bases like ammonia and fluoride ion
to be classified as bases, so long as they bond to protons.
The Bronsted-Lowry model implies that there is a relationship between
acids and bases (acids
transfer protons to bases) and allows us to define conjugate acids and
conjugate bases, as seen in
.
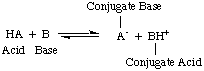
Figure %: The Bronsted model of acids and bases
You should note in the figure above that the conjugate acid
of the base,
BH
+, acts as an acid in the reverse reaction by donating a
proton to the conjugate base,
A
-, of the acid HA.
Despite the usefulness of the Bronsted-Lowry definition, there is an even
more general definition of
acids and bases provided by G. N. Lewis. The Lewis model of acids
and bases proposes that
an acid is an electron pair acceptor while a base is an electron pair
donor. This model of acidity
and basicity broadens the characterization of acid-base reactions to include
reactions like the
following which do not involve any hydrogen transfers. The nitrogen
atom in ammonia donates an electron pair to complete the
valence octet of boron.
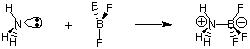
Figure %: Example of a Lewis acid-base reaction
Because we are more interested now in describing terms and processes
that
involve proton transfers (pH, titration), we will focus on the
Bronsted-Lowry definitions of acids and bases. We will leave
consideration of
the Lewis model of acids and bases for studying reactions in organic
chemistry.
Reactions of Acids and Bases with Water
As you may have noted already in the acid-base reactions above, we use arrows in
both reaction directions to indicate that these are equilibrium processes.
Proportions of reagents and products at equilibrium can be described by an
equilibrium constant. The
equilibrium constant given
in is for the reaction of an acid, HA, with water as shown.
Although water is a reactant in the above reaction and belongs in
the equilibrium
constant, its value of 55.6 M in aqueous solution is so large in comparison
with the change in water
concentration at equilibrium that we will assume that the value of
[H
2O] is constant.
Using that assumption, we will define the acid dissociation constant,
K
a, in to be the following:

Figure %: Definition of the acid dissociation constant
From the form of the above equation we can see that stronger acids,
those that dissociate
to a greater extent, will have larger values of
K
a whereas
weaker acids will have
smaller values of
K
a. A practical range for
K
a
values runs from
10
-12 for very weak acids to 10
13 for the strongest acids.
Knowing
this practical range of acidity constants will aid in judging how reasonable
your answers are when you calculate values for
K
a in problems.
In an analogous way, we define
K
b, the base constant in
to be the following:
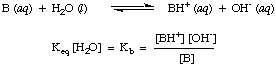
Figure %: Definition of the base dissociation constant
Stronger bases have larger values of
K
b while weaker bases
have
smaller values of
K
b.
K
b's of typical bases in inorganic
chemistry
tend to have a range of
values between 10
-11 and 10
3.
As you may have discovered in our above discussion, water can act as
both an acid and as a
base. For this reason water is said to be amphiprotic. Water is often
incorrectly termed amphoteric. An amphiprotic species like water can either
donate or accept a
proton.
Amphoteric species can both donate and accept hydroxide ions, as water
cannot. The following
reaction in , called the autoionization of water, has
the equilibrium constant
K
w defined in the manner of
K
a and
K
b. The dissociation constant
K
w for water
is 1 x 10
-14 at room temperature (298 K), and tends to rise with
higher temperatures.
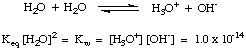
Figure %: The autoionization of water
Knowing that
K
w = 1 x 10
-14 is useful because the
relationship between
K
a and
K
b for a conjugate acid-base pair is
K
a *
K
b =
K
w. Therefore,
you can calculate the
K
a of the
conjugate acid of a base when given its
K
b. This point is
proved in below.
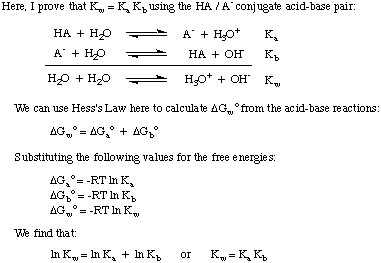
Figure %: The autoionization constant of water equals the product of the
acid and base dissociation constants of a conjugate acid-base pair.
From the proven expression, we see that strong acids (large
K
a's)
form weak conjugate bases and weak acids form strong conjugate bases.
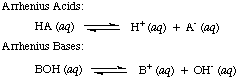
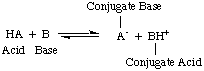
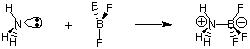
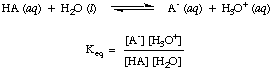

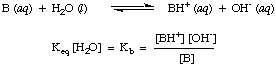
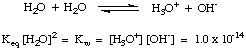
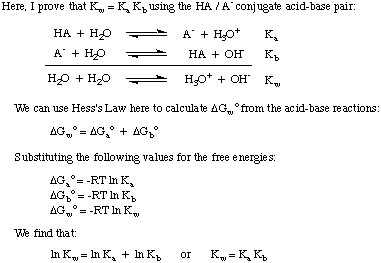
No comments:
Post a Comment