Let's explain First-Order Reaction.

 is the reaction rate and
is the reaction rate and  is the reaction rate coefficient. In first order reactions, the units of
is the reaction rate coefficient. In first order reactions, the units of  are 1/s. However, the units can vary with other order reactions.
are 1/s. However, the units can vary with other order reactions.



 Recall from calculus
Recall from calculus



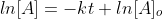
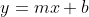
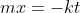
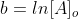



 Substitute
Substitute

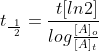
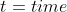
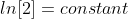

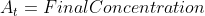
Example
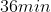 into t
into t
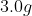 into Ao
into Ao
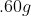 into At
into At
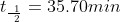
The Differential Form of the Rate Law
Rate law:

 is the reaction rate and
is the reaction rate and  is the reaction rate coefficient. In first order reactions, the units of
is the reaction rate coefficient. In first order reactions, the units of  are 1/s. However, the units can vary with other order reactions.
are 1/s. However, the units can vary with other order reactions.The Integrated Form of the Rate Law
First, write the differential form of the rate law.

Rearrange

Second, integrate both sides of the equation.



Upon integration, we get

Rearrange to solve for  and we get one form of the rate law
and we get one form of the rate law
 and we get one form of the rate law
and we get one form of the rate law
We can rearrange the equation above to:
Recall from Algebra y=mx +b is the equation of a straight line, which 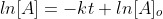 demonstrates.
demonstrates.
Now that we recall the laws of logarithms we can say that 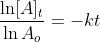 is at the time t with its final concentration of A and [A]o
is at time 0 and it is at its initial concentration of A and k is the
rate constant. Since, the logarithms of numbers do not have any units,
the product of -kt does not have units as well. This concludes that unit
of k in a first order of reaction must be time-1 . Examples of time-1 would be s-1 or min-1. Thus, the equation of a straight line is applicable to represent
is at the time t with its final concentration of A and [A]o
is at time 0 and it is at its initial concentration of A and k is the
rate constant. Since, the logarithms of numbers do not have any units,
the product of -kt does not have units as well. This concludes that unit
of k in a first order of reaction must be time-1 . Examples of time-1 would be s-1 or min-1. Thus, the equation of a straight line is applicable to represent 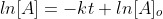
To test if it the reaction is a first
order reaction, plot the natural logarithm of a reactant concentration
versus time and see whether the graph is linear. If the graph is linear
and has a negative slope, the reaction must be a first order reaction.
To create another form of the rate law, raise each side of the previous equation to the exponent, e
Taking the natural log of both sides of the equation, we get the second form of the rate law

The integrated forms
of the rate law allow us to find the population of reactant at any time
after the start of the reaction. Plotting  with respect to time for a first-order reaction gives a straight line
with the slope of the line equal to -k. For more information on
differential and integrated rate laws.
with respect to time for a first-order reaction gives a straight line
with the slope of the line equal to -k. For more information on
differential and integrated rate laws.
 with respect to time for a first-order reaction gives a straight line
with the slope of the line equal to -k. For more information on
differential and integrated rate laws.
with respect to time for a first-order reaction gives a straight line
with the slope of the line equal to -k. For more information on
differential and integrated rate laws.Graphing First-order Reactions
The following graphs represents concentration of reactants versus time for a first-order reaction.


Plotting 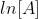 with respect to time for a first-order reaction gives a straight line with the slope of the line equal to -k.
with respect to time for a first-order reaction gives a straight line with the slope of the line equal to -k.

Relationship Between Half-life and First-order reactions
The half-life is a timescale by which the initial population is decreased by half of its orignal value, t1/2. We can represent the relationship by the following equation.

Using the integrated form of the rate law, we can develop a relationship between first-order reactions and the half-life.


Notice that, for first-order reactions,
the half-life is independent of the initial concentration of reactant.
This is unique to first-order reactions. Using an alternate half life equation of First Order Reaction would be
Thus, if a problem gave initial concentration,
final concentration and a time, it would be more applicable to use the
alternate half-life equation rather than: 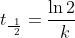
The practical
implication of this is that for A to decrease from 1 M to 0.5 M, it
takes just much time as it does for A to decrease from 0.1 M to 0.05 M
Example
If 3.0 g decomposes
for 36 min, the mass of A remaining undecomposed is found to be 0.60 g.
What is the half life of this reaction?
Solution:
Notice there are initial concentrations and final concentrations. This
should be a hint to use the alternate form of half life equation.
1) Plug in the values in the appropriate places
Note: Don't forget to multiply ln[2] in the equation.
After substituting the values into this equation, the half life is determined: