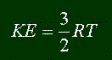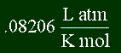Topics Covered
- Physics 'n' Energy
- Chemistry 'n' Energy
- Enthalpy
- Heat and Temperature
- Hess's Law
- Standard Enthalpies of Formation
Physics 'n' Energy
Thermochemistry is really all about energy. But first we've got to know what the hell energy is. The way that is used to describe it is mostly helpful in Physics. Therefore, I'm gonna describe it in physics first, and then the next section will be energy as it relates to our subject, chemistry. Heh...
Energy is the ability to do work. We've all heard that before. In actuality, it's sort of hard to define energy exactly. Even my normally adequate book admits that. Even though that's sorta fuzzy, you've used the term 'energy' before in everyday speech. It's... well... energy!!!
There are two flavors of energy; kinetic and potential. Let's start with kinetic energy. All matter that is moving has a certain amount of kinetic energy. In fact, if you actually visit my pages, I gave the formula for kinetic energy before:
It is dependant on mass and velocity. Note that it is proportional to the mass and the square of velocity. So if Ball A of some mass and velocity has a certain energy, and you have Ball B, with twice the velocity but only half the mass of Ball A, Ball B will still have twice as much kinetic energy, because velocity is squared. Kinetic energy can be changed, usually by a change in velocity (objects don't just change their mass, they're more likely to drop or gain in speed. Always exceptions, like if a rocket is losing fuel, then it's dropping in mass.) This change in kinetic energy is what is work. Like if a rocket is speeding up, then work is being done on it, because it's gaining kinetic energy. Likewise, if a rocket is slowing down, then the rocket is doing work, because it's losing kinetic energy. Yep, kinetic energy is some good stuff to have.
And then there's potential energy. It's harder to see, because it's the energy you can't see. You can 'see' the energy of a ball being thrown, you feel the energy transfer as you catch a ball. Potential energy is the energy available to the ball to convert to kinetic. In physics, the potential energy you talk about the most in mechanics is gravitational potential energy. This is simply the potential energy caused by gravity. Like if we take that same ball, and hold it off the side of the Empire State Building, it has the "potential" of gaining a lot of kinetic energy (by dropping it). It has a lot of potential energy, but no kinetic (it's not moving...yet.) But once you do, all that potential energy will be converted to kinetic, not all at once, but gradually. The ball speeds up faster and faster as it falls. A rule; the higher an object is, the more gravitational potential energy it has.
Now you don't have to know anything I have just said to do good in chemistry, just take away with you the Law of Energy Conservation. When you add the kinetic and potential energies of that ball at any time during its fall, they will be the same. Energy can't be gained or lost; it is always converted. Even when that ball hits the ground, and has lost all its kinetic and potential energy, that energy didn't really die, it just got converted to something else. The pavement (or car, wherever it landed doesn't matter) will have gained a slight increase in temperature, and that's where the energy went. It was dissipated as heat. The energy in a closed system always remains constant. I say closed system because if you considered the Earth a closed system, and then an outside source of energy (such as the falling of a great meteorite) came in, then the closed system will have more energy.
Energy comes in all sorts of shapes and sizes. There's heat (probably most important energy in chemistry), light, sound, mechanical, electrical, nuclear, matter/anti-matter reactions, the list goes on...
Let's talk chemistry.
Chemistry 'n' Energy
Finally, back to chemistry. In chemistry, reactions can give off heat, or absorb heat. Those that give off heat are called exothermic, and those that take in heat are called endothermic. In exothermic reactions, heat is a product (it's being formed), so a reaction of this kind might look like this:
A + B ---> C + D + heat
And similarly, if a reaction is endo, then it acts like a reactant (goes on the left side):
A + B + heat ---> C + D
Where does this heat flow from and to? In chem, you consider the entire Universe to be divided into two parts: the system, and the surroundings. The reaction is the system, and the surroundings is everything else. For the sake of pictures, pretty pictures, let's say the system is pink and the surroundings are purple. Here are illustrations of an exothermic and endothermic reaction. 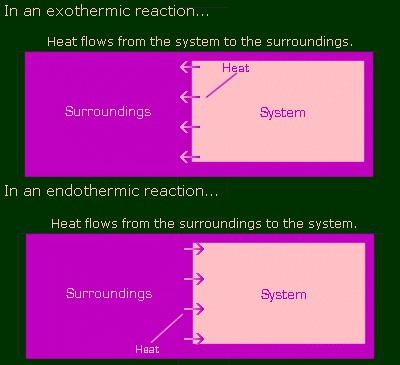
Where is this heat coming from? I said that the energy in a closed system is constant, so in an exothermic reaction, how come this heat is coming from nowhere? It's not really. Before the reaction, there was some potential energy stored in the bonds that made up the chemicals. When the bonds were broken and new bonds were formed to make new things, the energy of the new bonds was less than the energy they had previously. So that potential energy that was 'lost' was actually converted into heat, and that's where the heat came from. So the total energy level of the system and surroundings has in fact remained equal. This is in fact the first law of thermodynamics.
In chemistry, you always look at the system's point-of-view. The energy of the system can be changed in two ways: either change the heat of the system, or make it do work or work done on it. The energy change of the system is equal to the amount of heat added to it, plus the amount of work done on it. In other words (or symbols):
DE is the change of energy that happens to the system. q is the heat added, and w is the work done to it.
In thermodynamics, there is the concept of + and - signs. Since we are talking about point-of-view of the system, let's see how a + or - q/w means. If q is positive, that means the system will gain heat. If it's minus, then heat is being removed. That's simple enough. If w is positive, then work must be done on something as to make the energy of the system gain. If you do work on the system, then w will be positive. If you are expending energy, doing work, to make the system happy, then the system will gain energy. Similarly, if you're tired of doing work for this system that has done nothing for you, you can let the system do work for you. In which case w is negative, since it will be losing energy.
The unit of energy is the joule (Symbol: J). It is equal to the amount of kinetic energy a 2 kilogram ball has when traveling at 1 m/s. If bigger units are needed, the kilojoule (kJ) is used, and it's obviously 1000 joules.
I think we can do a problem or two here.
Example:
| Calculate the change in energy of a system if it did 14.3 kJ of work, while giving off 34.5 kJ of heat. Answer The most important part of this problem is to figure out the sign of w and q. It's giving off heat, therefore losing energy, so you can expect q to be negative. If it is doing work, then it is also losing energy in that way too, so w is negative as well. All you gotta do is add them up (-14.3 kJ + -34.5 kJ) and you will learn that the system has lost a total of 48.8 kJ. |
Let's talk about a way some system can do work. There's many ways, so we'll just cover one; gases. Think about what you do if you squeeze a balloon. Aren't you doing work to it? You are using your hard-earned energy to push this balloon in, and since energy is always transferred, it has to go somewhere, so it goes into the system of the gas in the balloon. So, if a gas is being crushed (volume is getting smaller), then work is being done to it, and w in that case is positive.
And if the volume is getting bigger, then w is negative. Why? Because the gas is pushing against the walls of the container, to give itself more room. So it's doing work, or losing energy.
The work being done is the pressure times the change of volume, like this:
w = PDV
This equation is not done yet. If volume is increasing (DV is positive) , then by equation it says that w is positive. But we just said that the system will be expending work in increasing its volume, so w should be negative when the change in volume is positive. A simple negative sign should fix that. And your final equation for the work done by a gas changing volume is:
You can see how I could incorporate this into a problem involving the first and second equations, but I won't. You get the idea.
Enthalpy
Aaah, yes, enthalpy. If you've just heard of enthalpy, you will have no idea what it is. When you're done with enthalpy, you'll still not have a clear good idea of what it is, but you will know how to do problems with it, and that's what is important.
The enthalpy of a system, H, is simply defined as:
H = E + PV
Enthalpy is equal to the total energy of the system, plus the pressure of the system times the volume of the system. It's sort of hard to grasp what enthalpy is, from that definition. Instead of enthalpy (H) itself, you will usually deal with a change of enthalpy (DH). And if pressure is constant, and the only work allowed to work on the system is through volume, then:
DH = q
Yep, you should think of enthalpy as sort of like heat. It's not heat exactly, but if those two conditions are met, then it is heat.
So if the change of enthalpy is increasing, that means it is gaining an increase of energy, and therefore is endothermic. If the change of enthalpy is decreasing, that means it is losing heat to the surroundings, or exothermic. Final thought: +DH = Endo, -DH = Exo.
How do you find the change of H? It's the enthalpy of the final products, minus the enthalpy of the reactants. Or...
DH = Hproducts - Hreactants
So if the products have less energy than reactants, then DH will be negative, indicating energy was lost. And vice versa. Heat and Temperature
I hope by now you realize the difference between heat and temperature. If you add heat (energy) to something, it will eventually start getting hotter and hotter. But the difference is, some substances will get hotter than others, if given the same energy. For example, on a hot summer day, everything around you might seem very hot (like the pavement, or your car), but if you go into a pool of water, it will be much cooler. Both the pavement and the water have received about the same amount of energy from the sun, but the pavement has gone through a much bigger temperature change than the water. Water is resistant to a change of temperature, in comparison to the pavement. Let's assume the temperature change is proportional to the energy it has received, so we can come up with an equation relating temperature and energy.
C is called the heat capacity and is different for different substances. This number C will tell you how hard is it for this substance to get hot. As you can figure, the bigger C is for some substance, the more energy is needed to get it hot.
We are forgetting one important factor; how much of the substance there is. The more there is, the more energy is needed to change its temperature. Putting all three things into account, we can come up with a more useful equation.
This is the same equation as the one before, but notice there's an m in the bottom. This is the definition for specific heat capacity. It's equal to the heat added divided by the mass of it and the change in temperature. As with the normal heat capacity, the bigger this number for some substancee, the harder it is to change its temperature. Water's specific heat capacity (or simply specific heat) is around 4.18 J/oC g.
Important! The mass in the above equation must be in grams. Well, if you use kilograms consistently, I guess it doesn't matter, but since specific heats in tables in books are given with grams, you should use grams.
Rearranging the above equation, you can solve for energy, since you can figure out the other three by measuring but not always energy.
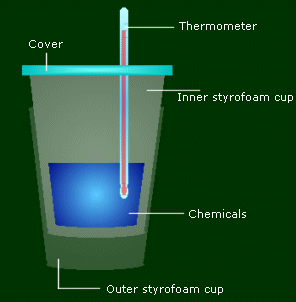
You use two styrofoam cups to make sure all the energy involved in the reaction is directly related to the temperature change of the chemicals, not the container/air. The cover on top is to make sure energy isn't leaving from the top. The thermometer is to measure the temp change.
How exactly do you do this? Let's say you're going to measure the energy given off by adding 50.0 mL of Chemical A and 20.0 mL of Chemical B. You can start with either one, let's start with A. Measure the weight of the cups beforehand. Put the 50.0 mL of A into the cup. Measure the temperature before. And then add B to it, and cover it and mix periodically. Keep on look at the temp, it should be changing. When it's done changing and stays the same, record the new temp. That's all there is to it. (And then measure the mass after the two things were put together.)
Then in q = s x m x T, you can subtract the masses to find the mass of the chemicals (in grams!). You can subtract the final temp minus the initial temp to change delta-T. But what about s? You can use water's specific temp, 4.18 J / K m. Why? Because most chemicals you'll be using won't be pure chemicals, but rather solutions. In case u forgot, that means they're dissolved in water, and it's not enough to significantly change the 4.18. So now you can find out how much heat is gained or lost.
There is one more concept here. Since pressure is constant, we can figure that the heat lost/gained is directly related to the enthalpy change. You could say that q = DH, but you'd be WRONG! In actuality, q = -DH. Why? Remember that enthalpy looks at energy from the point of the system. If heat was released (indicated by positive q), that means the system itself has lost it. Or if heat was absorbed (negative q), that means the system has gained it. So heat evolved and enthalpy change are just opposite of each other.
We've talked about constant-pressure cal. in detail; I'll just touch on constant-volume calorimetry here. Instead of keeping constant pressure, it tries to keep volume constant. That means you need a container that won't change volume. They're usually big strong metal cubes called a bomb calorimeter. I won't go through the specifics, because you probably won't be doing a lab with it; just be aware.
One last thing; in addition to specific heat capacity, there's the molar heat capacity. Instead of using grams to measure amount of substance, it uses moles. I won't give you equation, or any examples, because using specific heat is by far what everyone uses. Of course it has different units; instead of J/ K g, it's J/K mol.
Hess's Law
This has to do with enthalpy again. Yay. Remember that reactions have a certain enthalpy change with it: if it's positive, then the reaction will absorb energy; if negative, the reaction will give off energy. We can write the equation, and then the delta-H associated with it to the right of that. Like for example, to show the enthalpy change for the boiling of one mole of water to water vapor, you can write like this:
H2O (l) ---> H2O (g) DH = 44 kJ
So before one mole of water evaporates, 44 kJ of energy must be given to it.
I had to look up the 44 kJ in a table or something; there's no way anyone can just look at the equation and come up with it. But how about reactions that can't be found in a table? There are tons of reactions; you just can't carry a 30 pound book with you and look them all up. Hess's Law exists to make this easier for you. Technically, it means that the enthalpy change between two states is not dependant on the pathway it takes to get there. At first, this doesn't seem to help you one bit; but it means if you can add two or more equations to get the desired equation, then you can add their respective enthalpy changes to get the enthalpy change of this equation. There are two rules you will need to use in these problems. We'll use the equation above to illustrate these two rules:
- If you have to multiply each side of a reaction by some number X, then multiply the respective enthalpy change of that reaction by X also. So, if we needed to use not
H2O (l) ---> H2O (g), but twice that:2H2O (l) ---> 2H2O (g)Then we just multiply the delta-H of the original reaction by the same factor, two. Therefore the enthalpy change of 2 moles of water evaporating is 88 kJ.
- If you have to flip the equation around (the right side on the left and the left side on the right; switching the products and reactants; you get the idea) then just take the negative of the delta-H to get the delta-H of your new reaction. So if we wanted to find the enthalpy change of one mole of water vapor condensing to liquid water, like this:
H2O (g) ---> H2O (l)Then you just take the negative of the original delta-H, so the enthalpy change of the above equation is -44 kJ.
This is all you're going to learn in this section. But there are more involved problems. For the sake of simplicity, I'm not going to use real chemicals and enthalpies, because I don't know them. I'll just use chemicals "A", "B", and so forth. Have fun!
Example:
Please find the enthalpy change of
A + 2B ---> C
using the following information: #1: E ---> D + 2A, DH = 43.22 kJ
#2: B ---> F + [1/4]D, DH = 342 kJ
#3: 4F + E ---> 2C, DH = 2.2 kJ
Answer
This is about the hardest problem you might get. They can get harder, but I think they're past the scope of this course (I hope!) You have to add the equations below it to get the final equation. Where do we start? It's actually quite simple if you start with the beginning equation. We need a single A on the left. Well, look at the first given equation. It has a 2A in it, and no where else will you find an A. So you KNOW that the A on the left hand side MUST come from Equation #1.
You have to modify this equation so that the A's here look like what you want it to (the beginning equation). There's 2A's on the right. You want it to look like a single A on the left. So we can divide by two, and flip the equation.
A + [1/2]D ---> [1/2]E
Good! Now we have 1 A on the left. But remember that if we modify the equation, we have to modify the delta-H on this one too. You flipped it, so you can take the negative. So delta-H = -43.22 kJ. But we also divided by two, so divide this by two, and our new delta-H for #1 is -21.61 kJ. Keep this number in mind. Let's move on to the next figure in the beginning equation: 2B on the left. Well, out of the three givens, only #2 has a B anywhere. So that's where we must get our B's from. Problem is, the B is on the left like we want it, but there's only one. So multiply by two:
2B ---> 2F + [1/2]D
Coolio. Now we got 2B on the left. That's it. But remember to multiply original delta-H by 2, so the new one is 684 kJ. And finally, we need one C on the right. Since we used #1 and #2, we might suspect that C lies in #3. And of course, there it is, on the right of #3 like we want it. But there are 2 instead of one. What to do? Of course you divide by 2:
2F + [1/2]E ---> C
And then divide 2.2 kJ by 2, or 1.1 kJ for the new reaction.
Now what? Add the three new equations together (put all lefts on left, and all rights on right):
A + [1/2]D + 2B + 2F + [1/2]E ---> [1/2]E + 2F + [1/2]D + C
It looks like it's more fukt up than before, but look carefully and something magical happens; don't you have a [1/2]D on left and [1/2]D on right? You can subtract [1/2]D from both sides and cancel them. Same with 2F, and [1/2]E! So cancelling them, you have:
A + 2B ---> C
Wow, it's amazing, it's the beginning equation! Since all you did was add the modified equations to get the desired equation, all you have to do to find the desired enthalpy change is add the modified enthalpy changes: DH = -21.61 kJ + 684 kJ + 1.1 kJ = 663 kJ.
Woohoo! That's the enthalpy change for A + 2B ---> C. It's strange how the given equations just coincidentally cancelled out to make exactly the equation we were looking for. It's not coincidence; these type of problems must be planned out. It's a LOT harder making one of these problems than it is to solve them!
Standard Enthalpies of Formation
This has to do with enthalpy once again, as you might have brilliantly deduced from the title. Basically, the standard enthalpy change of formation of something is the enthalpy change of the reaction of the elements in their natural state coming together to form it under standard conditions. For example, the reaction of the formation of water is:
H2 (g) + [1/2]O2 (g) ---> H2O (l)
Note that hydrogen and oxygen must be in diatomic form and gaseous, because that is how they exist in a standard state. What is this standard state? In thermodynamics, the standard state is at 1 atmosphere and 25 oC (about room temperature). The standard enthalpies of formation for many substances can be found in a table. What is so useful about this? Let's say you have a reaction that you have to find the enthalpy change in the standard state. But instead of before where we had all those given equations to mess around with, you are just given a table of standard enthalpies of formation. How will you do this? Here's the equation:
DHo = SnpDHof p - SnrDHof r
You might be staring at this mess and wondering what the hell it means, but basically it says that you add up the standard enthalpies of formation on the right side (multiplying with respective coefficients) and subtracting the standard enthalpies of formation on the left side (ditto.) You know, it just might be easier if you saw this one in an example. Once again, I am using A's, B's, C's, and D's, but in a real problem you'll get real things to use.
Example:
Find the change of enthalpy of the following equation (under standard conditions):
A + 2B ---> 2C + 3D
Using the following standard enthalpies of each substance: A: 34 kJ/mol
B: 45 kJ/mol
C: 22.3 kJ/mol
D: 56 kJ/mol
Answer
Firstly, I should explain the kJ/mol. Enthalpies are supposed to be in joules, or kilo joules, right? But for formation, the enthalpy depends on how much you are forming. So, for A, it takes 34 kJ to form one mole of A. So if you were forming 2 moles of A, the enthalpy would be twice as much, or 68 kJ. If you were making 3.45 moles of B, the enthalpy of formation would be 155.25 kJ (3.45 mol x 45 kJ/mol).
Ok, let's start. The formula says to take the stuff on the right, and subtract the stuff on the left. So start with the first thing on the right, 2C. The standard enthalpy for C is 22.3 kJ/mol, but we have 2 of them. So the enthalpy for 2C is 44.6 kJ.
Next up on right; 3D. D's enthalpy of formation is 56 kJ/mol, and 3 of them makes 168 kJ.
So you add up to get total enthalpy on right, which is 44.6 kJ + 168 kJ = 212.6 kJ. Keep this in mind.
Now we go to the left. First thing on left: A. There's only one of A, so total enthalpy is 34 kJ.
Lastly, there are 2 B's. Enthalpy of 1 B: 45 kJ, but there are two, so total is 90 kJ.
Now you add up all the enthalpies on the left. So that is 34 kJ + 90 kJ = 124 kJ.
Last step: Subtract total of left from total on right. 212.6 kJ - 124 kJ = 88.6 kJ.
And there's your answer!
One note: You can only do this if the reaction is to take place in standard conditions. I don't know if I mentioned this before, but enthalpy is dependant on temperature and pressure. So if the reaction above took place at 10 degrees Celsius and at 30 atm's, you couldn't do it this way. Of course, if they gave you enthalpies of formation at those conditions, then go right ahead. (They have to match.)